Metody Numeryczne: listopada 2015

Interpolacja liniowa – szczególny przypadek aproksymacji za pomocą funkcji liniowej.

Aproksymacja (łac. approximare – przybliżać) – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi. Często stosowana w przypadku szukania rozwiązań dla danych uzyskanych metodami empirycznymi, które mogą być obarczone błędami.

Jeśli x określa wartość z przedziału x0 < x < x1, a y0 = f(x0) i y1 = f(x1) tablicę wartości danej funkcji, oraz h = x1 - x0 odstęp pomiędzy argumentami, wówczas liniową interpolację wartości L(x) funkcji f otrzymuje się jako:

Interpolacja liniowa

Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n przyjmującym w n+1 punktach, zwanych węzłami interpolacji, wartości takie same jak przybliżana funkcja.

Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.

Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x), ciągłą na przedziale domkniętym, można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.

Metoda interpolacji polega na:

wybraniu n+1 punktów x0,x1,...,xn należących do dziedziny f, dla których znane są wartości

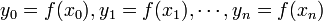
$y_0=f(x_0),y_1=f(x_1),\cdots ,y_n=f(x_n)$
znalezieniu wielomianu W(x) stopnia co najwyżej n takiego, że

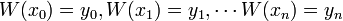
$W(x_0)=y_0,W(x_1)=y_1,\cdots W(x_n)=y_n$

Interpretacja geometryczna – dla danych n+1 punktów na wykresie szuka się wielomianu stopnia co najwyżej n, którego wykres przechodzi przez dane punkty.

Znajdowanie odpowiedniego wielomianu

Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:

Dla pierwszego węzła o wartości f(x0) znajduje się wielomian, który w tym punkcie przyjmuje wartość f(x0), a w pozostałych węzłach x1,x2,...,xn wartość zero.
Dla kolejnego węzła znajduje się podobny wielomian, który w drugim węźle przyjmuje wartość f(x1), a w pozostałych węzłach x0,x2,...,xn wartość zero.
Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego.
Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego.
Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym.

Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.

Wielomian Lagrange'a

Postać Lagrange'a wielomianu to jedna z metod przedstawiania wielomianu, wykorzystywana często w zagadnieniach interpolacji. Dla wielomianu stopnia n wybiera się n+1 punktów – x0,x1,...,xn i wielomian ma postać:

Ponieważ
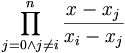$\prod_{j=0 \and j\ne i}^n \frac{x-x_j}{x_i-x_j}$ jest równy 1 dla x równego xi (licznik i mianownik są równe), 0 zaś dla wszystkich innych xj (licznik jest równy zero), można łatwo za pomocą postaci Lagrange'a interpolować dowolną funkcję:

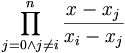$L_f(x) = \sum_{i=0}^n f(x_i) \prod_{j=0 \and j\ne i}^n \frac{x-x_j}{x_i-x_j}$

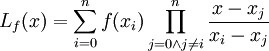
Wielomian ten będzie się zgadzał z funkcją f we wszystkich punktach xi.

Szybka transformacja Fouriera

Szybka transformacja Fouriera (ang. fast Fourier transform, FFT) – algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do niej odwrotnej.

Czasem używana jest też forma szybka transformata Fouriera w odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a transformata wynikiem tego przekształcenia.

Niech x0, ...., xN-1 będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem:

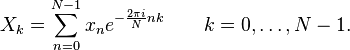
$X_k = \sum_{n=0}^{N-1} x_n e^{-{2\pi i \over N} nk } \qquad k = 0,\dots,N-1.$

Obliczanie tych sum za pomocą powyższego wzoru zajęłoby O(N2) operacji.

Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką transformację Fouriera bazują na metodzie dziel i zwyciężaj, rekurencyjnie dzieląc transformatę wielkości N = N1N2 na transformaty wielkości N1 i N2 z wykorzystaniem O(N) operacji mnożenia.

Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany sygnał) musi mieć długość N=2^k, gdzie k to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe.

Złożoność obliczeniowa Szybkiej transformacji Fouriera wynosi O(N \log_2 N), zamiast O(N^2) algorytmu wynikającego wprost ze wzoru określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG, MP3 itd.) do kompresji.

czwartek, 19 listopada 2015

Interpolacja liniowa